AC自动机用于解决下述问题及其同类问题:

给定一系列模式串和一个文本串，判断有多少模式串出现在文本串中，给出数目和对应模式串的出现位置。

主要思想

AC自动机主要用到了Trie树和KMP算法的思想。

构造

我们首先将所有模式串构建成一个Trie树，构建方法与普通Trie树的构建方法没有区别。

AC自动机的树结构主要是比Trie树多一个fail指针（类似于KMP算法的next数组）。

class AcNode {
public:
    AcNode* m_childs[26] = { nullptr };
    bool m_is_end;  // 是否是单词边界
    char m_c;

    // 新增内容
    AcNode* fail = nullptr; 
};

该fail指针是AC自动机的核心，它表示当前树节点匹配失败，下一个要尝试匹配的树节点。实际上，fail指针所指的树节点所构成的字符串是当前树节点构成字符串的后缀。

Fail指针的求法

root的孩子的fail指针是root, 对于其他节点，其fail指针是父亲的fail指针所指的树节点的孩子中和当前节点字母相同的节点。如果不存在这样的节点，则尝试寻找fail指针所指树节点的fail指针所指的节点有无这样的节点，直到root节点。

比较绕口，举个例子：

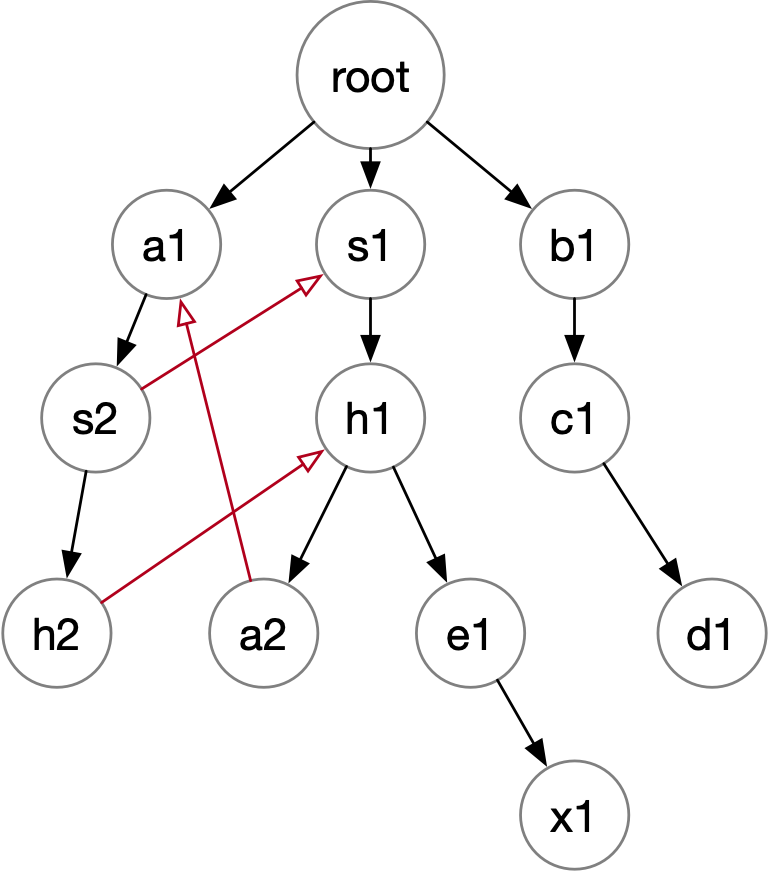图1. Fail指针求解
图1. Fail指针求解

如图1所示，h2的fail指针是h1。求解过程是h2 -> s2 -> s2.fail = s1 -> h1。

匹配

匹配的时候也很简单，对于文本串中的每个字母，从AC自动机的root开始尝试匹配。

  • 匹配成功，则跳至其fail指针，继续尝试匹配，直到跳回root指针 - 处理类似she同时包含she和he的情况。
  • 匹配失败，也要跳到其fail指针继续尝试匹配。

根据需要记录匹配成功的数目，位置以及对应的模式串。

C++实现

具体实现参见ac_automaton.cpp，这里解释一下求fail指针的build函数。

void build() {
    queue<AcNode*> q;
    for(int i=0; i<26; i++) {
        if(root->m_childs[i] != NULL) {
            root->m_childs[i]->fail = root;
            q.push(root->m_childs[i]);
        } else { root->m_childs[i] = root; }
    }
    AcNode* current;
    while(!q.empty()) {
        current = q.front();
        q.pop();
        for(int i=0; i<26;i ++) {
            if(current->m_childs[i] != NULL) {
                current->m_childs[i]->fail = current->fail->m_childs[i];
                q.push(current->m_childs[i]);
            } else {
                current->m_childs[i] = current->fail->m_childs[i]; // 路径压缩
            }
        }
    }
}

要点:

  1. 使用BFS逐层的求解fail指针。
  2. 不存父亲指针，遍历到当前节点时，计算子节点的fail指针。
  3. 注意把root指针的所有“空”孩子设置为root，否则容易在计算孩子的fail指针时发生segemntation fault，current->fail->m_childs[i]这个表达式fail可能是root。
  4. 不用递归寻找符合要求的fail指针, 使用类似并查集的思想进行路径压缩。

路径压缩

核心为这行代码:

current->m_childs[i] = current->fail->m_childs[i];

当current->fail->m_childs[i] = NULL的时候，这行代码将m_childs[i]置为其fail->m_childs[i]，由于是逐层求解fail的，因此当fail->m_childs[i]也等于NULL的时候，其值会在之前被设置成其fail->m_childs[i]。

因此current->fail->m_childs[i];总是指向满足要求的节点或者root。

满足要求: fail指针所指的树节点所构成的字符串是当前树节点构成字符串的后缀。

参考资料

  1. [洛谷日报第44期]强势图解AC自动机: Link