Steepest Descent && Conjugate Gradient

April 25, 2022

这是一篇主要介绍Conjugate Gradient (CG)的笔记，当然为了引入CG，也会一并介绍其“前身” Steepest Descent。

本文主要参考这篇论文： An Introduction to the Conjugate Gradient Method Without the Agonizing Pain

It is definitely the best paper to understand the steepest descent conjugate gradient method, which save me a lot of time, thanks god. And it is written in 1994, pretty cool, right? 🧐

类似的知乎： https://zhuanlan.zhihu.com/p/64227658

Introduction #

Well, let’s begin with a short outline of this paper:

首先，我们需要了解CG要求解的问题，CG是一个迭代求解大规模线性方程组的方法，即我们要求:

$$ Ax = b $$

其中x是我们要求的一个向量，b是一个已知向量，A是一个已知的 square, symmetric, positive-definite 的矩阵。

The Quadratic Form #

二次型是一个标量二次函数，即输入是一个向量x，输出一个标量，它的形式如下：

$$ f(x) = \frac{1}{2}x^T A x - b^T x + c $$

对$f(x)$求导，我们有：

$$ f'(x) = \frac{1}{2}A^Tx + \frac{1}{2}Ax -b $$

当A是对称矩阵时，我们有:

$$ f'(x) = Ax - b $$

不难得出，当A是对称矩阵时，原问题$Ax=b$的解就是二次型导数为0的点，也即极值点。因此，我们可以通过求解二次型的极值点找到$Ax=b$的解。

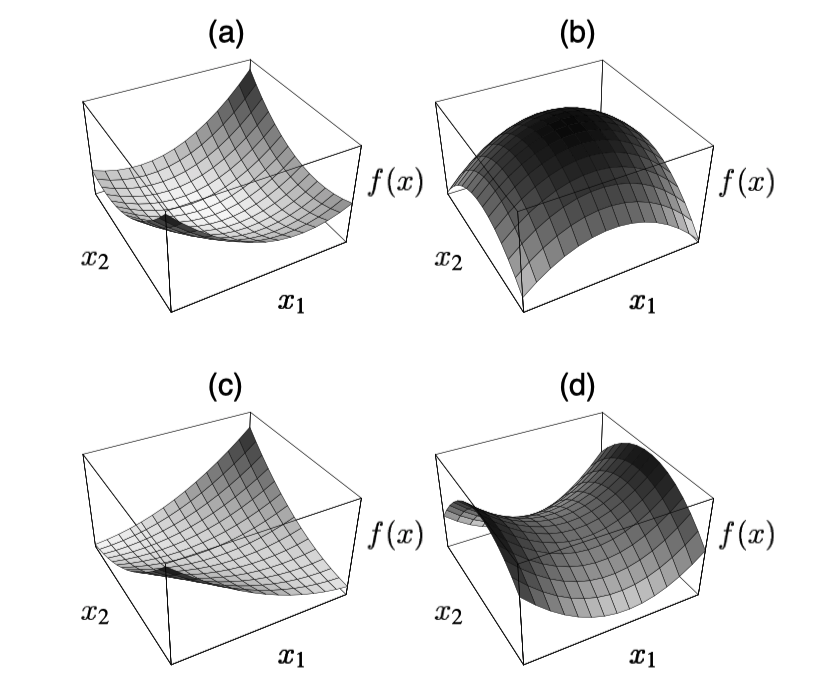
进一步的，如果A是正定（postive definite）矩阵，二次型的极值点是它的最小值点，因此我们可以通过最小化 $f(x)$ 找到 $Ax=b$ 的解。

当A矩阵是正定矩阵时，二次型有最小值，如a所示，如果是负定矩阵，则如b所示。原论文 Figure 5。

Steepest Descent #

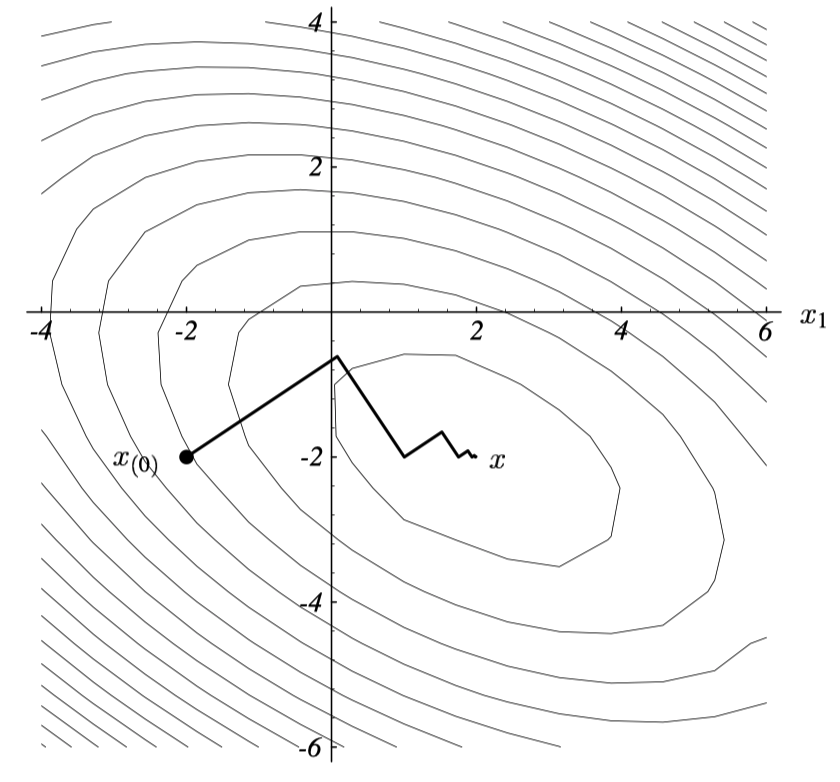
回顾，我们现在需要做的是找出二次型的最小值。

首先，基于迭代的求最小值的方法思路都是从一个随机解 $x_0$开始，不断更新，得到 $x_1, x_2, …$，直到与真实值足够接近。（用$r=Ax-b$判断）

Steepest Descent 也是基于迭代的方法，它是梯度下降的一个改进，即从初始点出发，每次都朝负梯度方向更新。

$$ -f'(x_i) = b - Ax_i $$

我们定义 residual 和 error $$ r_i = b - Ax_i $$ $$ e_i = x_i -x $$

则每次更新公式为：

$$ x_{i+1} = x_i + \alpha r_i $$

现在一个问题是，我们知道更新的方向，但我们要走多远呢？即 $\alpha$ 要如何选取。

Steepest Descent的思路是，每次更新都取从负梯度方向出发能够的到达的最低点。如下图a,b所示。

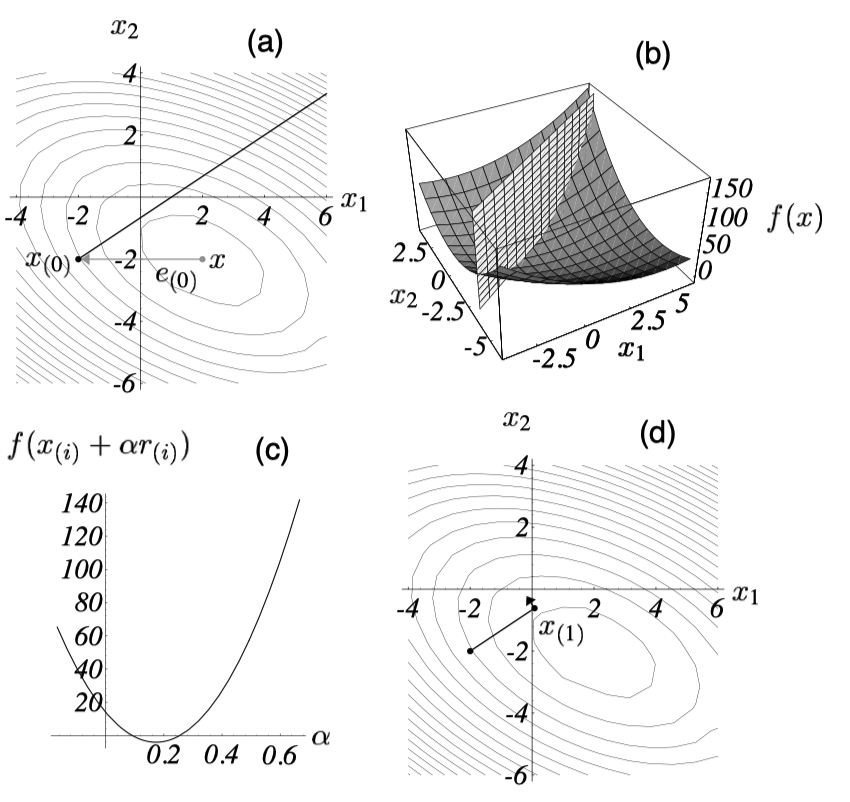
从数学上，我们的目标就是找到一个 $\alpha$ 使得 $f(x_{i+1})$ 最小。回忆，因为A是正定的，所以 $f$ 的极值点就是最值点，因此我们可以通过导数 $\frac{\partial f(x_{i+1})}{ \partial \alpha}$ 为0，求得 $\alpha$。

应用复合函数求导： $$ \frac{\partial f(x_{i+1})}{ \partial \alpha} = \frac{\partial f(x_{i+1})}{ \partial x_{i+1}} \frac{\partial x_{i+1}}{ \partial \alpha} $$

其中 $\frac{\partial f(x_{i+1})}{ \partial x_{i+1}} = f'(x_{i+1}) = - r_{i+1}$， $ \frac{\partial x_{i+1}}{ \partial \alpha} = r_i$

令导数为0，我们有（为了简化表达式，这里用1表示i+1，0表示i）：

$$ \begin{aligned} r_{(1)}^{T} r_{(0)} &=0 \\ \left(b-A x_{(1)}\right)^{T} r_{(0)} &=0 \\ \left(b-A\left(x_{(0)}+\alpha r_{(0)}\right)\right)^{T} r_{(0)} &=0 \\ \left(b-A x_{(0)}\right)^{T} r_{(0)}-\alpha\left(A r_{(0)}\right)^{T} r_{(0)} &=0 \\ \left(b-A x_{(0)}\right)^{T} r_{(0)} &=\alpha\left(A r_{(0)}\right)^{T} r_{(0)} \\ r_{(0)}^{T} r_{(0)} &=\alpha r_{(0)}^{T}\left(A r_{(0)}\right) \\ \alpha &=\frac{r_{(0)}^{T} r_{(0)}}{r_{(0)}^{T} A r_{(0)}} . \end{aligned} $$

事实上 Steepest Descent 每次更新的方向都与上一步的方向正交的。

这是因为每一步更新的时候都是从负梯度方向走到最低点，如果停下来的位置梯度不与更新梯度正交，那么这个位置就不是最低点，因为这个位置在更新梯度上还有一个不为0的分量。